MATEMATICAS 2. TRIGONOMETRIA. COBAO 04 EL TULE. XOCHITL FERNANDA ALONSO PRUDENTE

                                                         MATEMÁTICAS 2

                            TRIGONOMETRIA 

                           COBAO 04 EL TULE

                             SEMESTRE 2020-A

  ALUMNA: XOCHITL FERNANDA ALONSO PRUDENTE
                            GRUPO:205

PROFESOR: ALEJANDRO ENRIQUE VASQUEZ MARTINEZ


LISTA DE TRABAJO DE MATEMÁTICAS 2:

RESÚMENES DE CONCEPTOS:

+clasificacion y formas de medicion de angulos. conversion de angulos
+razones trigonometricas
+angulos de elevacion y depresion
+mapa cognitivo de aspectos comunes entre los conceptosde los angulos de elevacion y       depresion
+resumen de las caracteristicas para la medicion de angulos en trigonometria (angulos de referencia)
+mapa cognitivo de secuencias para representar y calcular angulos de referencias
+resumen de circulo unitario y funciones trigonometricas
+matriz de clasificacion de las caracteristicas de las graficas de funciones trigonometricas
+resumen de ley de senos y ley de los cosenos
+mapa cognitivo tipo satelite de la ley de los senos y cosenos

BANCO DE PROBLEMAS:

+anfonssi y flores Meyer, trigonometria rectilinea. angulos de elevacion y depresion pag.61,62,63
+anfonssi y flores meyer.trigonometria rectilinea.seno 48,49,50
+anfonssi y flores meyer. trigonometri rectilinea. coseno 51
+anfonssi y flores meyer. trigonometri rectilinea. tangente 52,53
+anfonssi y flores meyer. identidades y ecuaciones 127,131
+fuenlabrada, samuel.geometria y trigonometria.ed.McGraw Hill.ecuaciones 135,136
+anfonssi y flores meyer ley de senos y cosenos. pags.161,162
+guia de matematicas 2.COBAO.Pags.134,136,147
+guia de matematicas 2.COBAO.pags. 148,149
+guia de matematicas 2 COBAO.pag.155
+guia de matematicas 2. COBAO. pag.187
+guia de matematicas 2. COBAO.pags. 191,192
+guia de matematicas 2. COBAO. PAGS. 211,212

PROYECTOS:

+tabla de valores de razones trigonometricas 
+angulos de elevacion y depresion
+graficas de funciones trigonometricas
+tabla de identidades trigonometricas
+figura de papiroflexia.calculo de angulos y lados de triangulos no rectangulos 








CLASIFICACION Y FORMAS DE MEDICION DE ANGULOS.CONVERSION DE ANGULOS

El ángulo es la figura formada entre dos rectas que se cruzan en un punto. Las rectas -que podrían también ser semirrectas o segmentos- reciben el nombre de lados del ángulo y el punto donde se cortan es el vértice del ángulo. De hecho, dos rectas que se cruzan forman cuatro ángulos.

Hay varias maneras de referirnos a un ángulo, podemos darle el nombre del vértice agregando el símbolo de ángulo: $\angle O$, o nombrarlo con una letra griega ($\alpha ,\beta ,\delta ,\gamma ,\eta ,ϵ,$ etc.), escrita dentro del ángulo señalándolo con una curva entre las dos rectas. Si el ángulo está determinado por segmentos, podemos identificarlo señalando los puntos que los determinan: el punto central será el del vértice del ángulo y los de los extremos indicarán el sentido en el que lo mediremos. Observa en la siguiente figura,

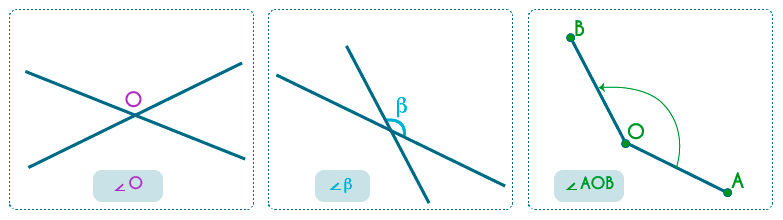
Tenemos el ángulo $\angle O$, el ángulo $\beta$ y el ángulo $\angle AOB$, considerado en sentido positivo es decir, el giro contrario a las manecillas del reloj.

Para medir un ángulo es necesario definir una unidad de medida. Las más usadas son el grado sexagesimal, comúnmente llamado grado, y el radián. El grado sexagesimal es la medida de un ángulo cuya abertura es $\frac{1}{360}$ de la circunferencia. En este caso se considera como vértice del ángulo el centro de la circunferencia y sus lados son dos radios. Por otra parte, para medir un radián también consideramos una circunferencia pero de radio 1. Y nuevamente consideramos el ángulo con vértice en el centro de la circunferencia y cuyos lados son dos radios. La medida del ángulo en radianes será la longitud del arco que el ángulo subtienda en la circunferencia.

La relación que guardan entre sí estas medidas es$$\pi \sim 180°$$y con ella podemos convertir grados a radianes o radianes a grados. Las expresiones que resultan son:

RAZONES TRIGONOMETRICAS

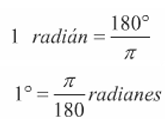
Seno

El seno del ángulo B es la razón entre el cateto opuesto al ángulo y la hipotenusa. Se denota por sen B.

Coseno

El coseno del ángulo B es la razón entre el cateto adyacente o contiguo al ángulo y la hipotenusa. Se denota por cos B.

Tangente

La tangente del ángulo B es la razón entre el cateto opuesto al ángulo y el cateto adyacente al ángulo. Se denota por tan B o tg B.

Cosecante

La cosecante del ángulo B es la razón inversa del seno de B.

Se denota por csc B o cosec B.

Secante

La secante del ángulo B es la razón inversa del coseno de B.

Se denota por sec B.

Cotangente

La cotangente del ángulo B es la razón inversa de la tangente de B.

Se denota por cot B o ctg B.

ANGULOS DE ELEVACION Y DEPRESION

El término ángulo de elevación denota al ángulo desde la horizontal hacia arriba a un objeto. Una línea de vista para el observador estaría sobre la horizontal.

El término ángulo de depresión denota al ángulo desde la horizontal hacia abajo a un objeto. Una línea de vista para el observador estaría debajo de la horizontal.

Dese cuenta que el ángulo de elevación y el ángulo de depresión son congruentes .

ASPECTOS COMUNES ENTRE LOS CONCEPTOS DE LOS ANGULOS DE ELEVACION Y LOS ANGULOS DE DEPRESION

Ángulo de elevación
Es el ángulo vertical  (agudo) formado por la línea horizontal y la línea visual cuando el objeto o punto observado  se encuentra arriba de la línea horizontal.
Ángulo de depresión
Es el ángulo vertical  (agudo) formado por la línea horizontal y la línea visual cuan el objeto o punto observado  está debajo de la línea horizontal.

ANGULOS DE REFERENCIA

Un ángulo de referencia es un ángulo agudo positivo que representa un ángulo θ de cualquier medida. Éste es el ángulo más pequeño formado entre el lado terminal de θ y el eje x. Siempre utilizamos éste último como su marco de referencia y el procedimiento para medirlo dependerá del cuadrante en el que se encuentre θ.

DEFINICIÓN

Sea θ un ángulo en posición estándar; el ángulo de referencia para éste es el ángulo positivo agudo (θR) que el lado terminal de θ hace con el eje x.

FÓRMULA PARA EL ÁNGULO DE REFERENCIA ΘR

θR se mide en base de la posición de un ángulo dado en cualquiera de los cuatro cuadrantes de un plano rectangular

SECUENCIAS PARA REPRESENTAR Y CALCULAR ANGULOS DE REFERENCIA

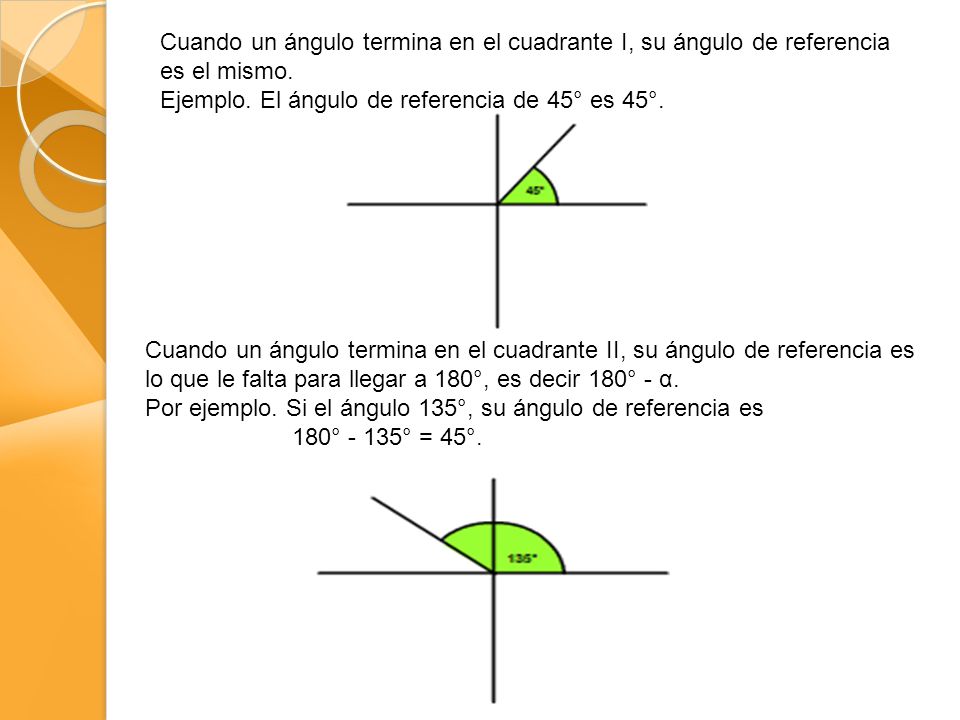
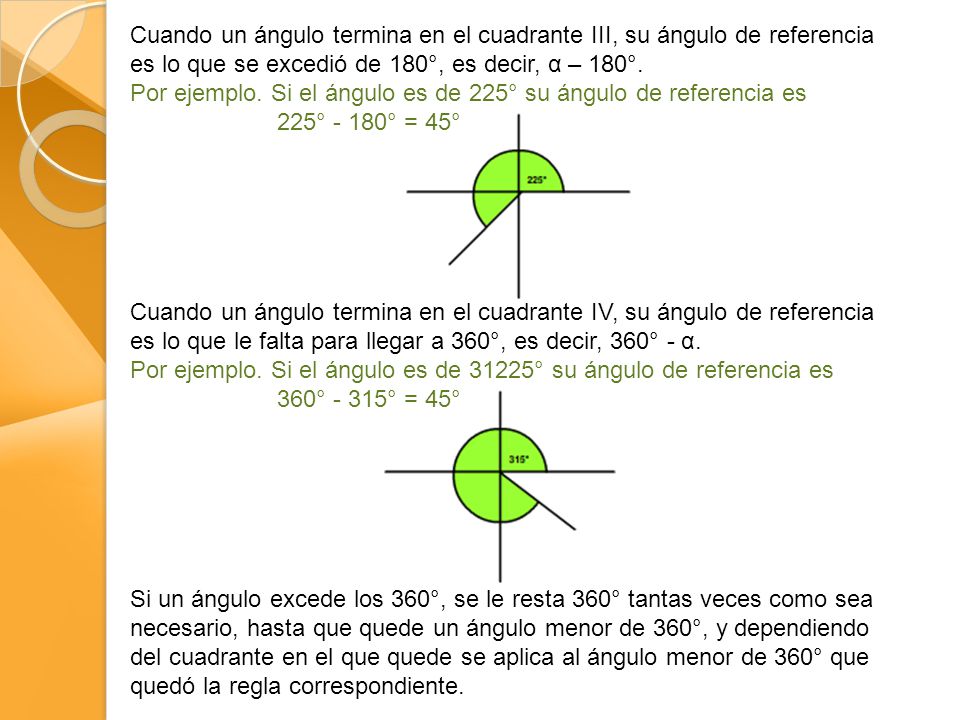
La definición en el círculo unitario nos permite extender el dominio de seno y coseno a todos los números reales. El proceso para determinar el seno o coseno para cualquier ángulo $\theta$theta es como sigue:

1. Empezando en $(1,0)$left parenthesis, 1, comma, 0, right parenthesis, nos movemos a lo largo del círculo en sentido contrario a las manecillas del reloj hasta que el ángulo que se forma entre tu posición, el origen y el eje $x$x positivo sea igual a $\theta$theta.
2. $\sin(\theta)$sine, left parenthesis, theta, right parenthesis es igual a la coordenada $y$y de tu punto, y $\cos(\theta)$cosine, left parenthesis, theta, right parenthesis es igual a la coordenada $x$x.

$y$$x$$(\cos(\theta),\sin(\theta))$$\theta$$O$$\cos(\theta)$$\sin(\theta)$$\small 1$$\small 1$$\small{-1}$$\small{-1}$

Las demás funciones trigonométricas pueden evaluarse a partir des su relación con seno y coseno.

CLASIFICACION DE LAS CARACTERISTICAS DE LAS GRAFICAS DE FUNCIONES TRIGONOMETRICAS

Las gráficas de las funciones trigonométricas  poseen propiedades matemáticas muy interesantes como máximo, mínimo, asíntotas verticales, alcance y periodo entre otras.

Es necesario estudiar la forma de la gráfica de cada función trigonométrica. Esta forma está asociada a las características particulares de cada función. En la figura de abajo se presentan algunas gráficas de funciones trigonométricas.

     Al establecer relaciones entre dos conjuntos mediante las funciones trigonométricas se establecen relaciones como y=sen(x), y=cos(x), y=tan(x), y=cot(x), y=csc(x) o y=sec(x). La expresión en el paréntesis se denomina argumento de la función (dominio) mientras que y representa el alcance (imágenes).

     Las gráficas de estas funciones se extienden sobre los ejes coordenados, si es sobre el eje de x, tienen la característica de repetirse por intervalos. Esto significa que cada cierta cantidad de radianes, una parte de la gráfica de la función es la misma (periodo). La extensión sobre el eje de y se conoce como alcance. Veamos cada función particular en detalle.

     El modelo de las gráficas de las funciones trigonométricas se obtiene evaluando la función para ángulos que forman una revolución completa.

Gráfica de la Función Seno del ángulo

El modelo de la gráfica de la función seno del ángulo se puede obtener transfiriendo puntos del círculo unitario al sistema rectangular de coordenadas. Recuerde que la función seno del ángulo utiliza la y de los arcos del círculo unitario. El ciclo fundamental de la función seno del ángulo comienza en 0 y termina en 2π. En la figura de abajo se observa la relación entre la circunferencia unitaria y la gráfica de la función seno del ángulo x. Esta figura muestra el desarrollo de la gráfica de la función seno del ángulo x a partir de la circunferencia unitaria.

Esta función tiene un punto máximo y un punto mínimo en el ciclo fundamental de su gráfica. Veamos las características de la gráfica de la función y=sen(x).

Su dominio es el conjunto de números reales

Su alcance es el conjunto de números mayores o iguales que menos uno hasta los números menores o iguales que uno.

Su intercepto en el eje de y es el punto (0,0).

El eje de x será el eje de referencia.

El punto máximo del ciclo fundamental tiene coordenadas (π/2,1).

El punto mínimo del ciclo fundamental tiene coordenadas (3π/2,-1).

Su periodo es 2π.

Ejemplo: (presione aquí para verlo en forma interactiva)

Trace la gráfica de la función f(x) = -2sen(x+π/2) + 1.

Solución:

Características:    El alcance es el conjunto de imágenes correspondientes al intervalo [-1, 3].    La intersección en el eje de y es el punto (0, -1).    Tiene máximo en el punto (π, 3) y el mínimo en el punto (0, -3) .    El periodo de esta función es 2π .

Gráfica de la Función Coseno del ángulo

El modelo de la gráfica de la función coseno del ángulo se puede obtener transfiriendo puntos del círculo unitario al sistema rectangular de coordenadas. Recuerde que la función coseno del ángulo utiliza la x de los arcos del círculo unitario. El ciclo fundamental de la función coseno del ángulo comienza en 0 y termina en 2π. En la figura de abajo se observa la relación entre la circunferencia unitaria y la gráfica de la función coseno del ángulo x. Esta figura muestra el desarrollo de la gráfica de la función coseno del ángulo x a partir de la circunferencia unitaria.

Esta función tiene un punto máximo y un punto mínimo en el ciclo fundamental de su gráfica. Veamos las características de la gráfica de la función y=cos(x).

Su dominio es el conjunto de números reales

Su alcance es el conjunto de números mayores o iguales que menos uno hasta los números menores o iguales que uno.

Su intercepto en el eje de y es el punto (0,1).

El eje de x será el eje de referencia.

El punto máximo del ciclo fundamental tiene coordenadas (0,1) y (2π,1).

El punto mínimo del ciclo fundamental tiene coordenadas (π,-1).

Su periodo es 2π.

 LEY DE SENOS Y LEY DE LOS COSENOS

ENUNCIADO DE LA LEY DE LOS SENOS.

“En todo triangulo se cumple que la razón del seno de un ángulo con su lado opuesto es igual a la razón de cualquiera de los otros ángulos con su lado opuesto.”

Lo anterior se expresa así:

LEY DE LOS COSENOS.

“En todo triangulo se cumple que conociendo 2 lados y el ángulo comprendido entre ellos, se puede conocer el tercer lado”

Esto supone 3 posibilidades:

SOLUCIÓN DE TRIÁNGULOS.

 Resolver un triángulo significa conocer todos los ángulos y los lados de este. Para resolver un triángulo se pueden utilizar la ley de senos, la ley de cosenos o también el teorema de Pitágoras.

 Veamos la aplicación de estas leyes en los siguientes ejemplos.

Ejemplos:

 Resolver los siguientes triángulos:

Hallar los ángulos α   ,  β  , θ

Luego de hallar θ:

 Como los ángulos interiores de todo triangulo suman 180⁰, entonces:

 θ=180⁰-(α+β)

θ=180⁰-(37.40⁰+84.93⁰)=57.67⁰

 2) 

No se conocen “a”, β ni α

           ANFONSSI FLORES MEYER, TRIGONOMETRIA RECTILINEA. ANGULOS DE ELEVACION Y DE DEPRESION  61,62,63

1.¿que angulo forma la visual al sol con el horizonte , si un edificio de 15m de altura proyecta una sombra de 36m?





2.desde la punta B de una torre, el angulo de depresion de la punta D de otra torre, que dista 25m de la primera , es de 25°. si la torre mas alta mide 62m,¿cual es la altura de la menor?




3.desde una embarcacion P se ve un faro F y una casa C, en las direcciones este y sur-sureste. sabiendo que la casa y el faro distan 2km , hallese la distancia de la embarcacion al faro




4.dos observadores distan de 250m. si uno de ellos viera un globo en su cenit(es decir, en la vertical de su lugar de observacion), y el otro lo viera a  40°20°sobre el horizonte¿cual seria la altura del globo?





5. una escalera de 12m de largo, apoyada contra un edificio forma un angulo de elevacion de 68°. hallese la altura del edificio, sabiendo que el extremo de la escalera toca la cima del mismo.





6.el faro de la torre eifel esta situado a 300m de altura¿que distancia hay que recorrer,a partir del pie y horizontalmente, para que el angulo de elevacion del faro sea de 25°?



7.determinar la diferencia de nivel entre dos puntos, de los cuales uno esta situado en una llanura y el otro en una altura inaccesible.segun el mapa,la distancia aparente entre dos puntos es de 200m, y el angulo de elevacion del punto mas alto es de 20°





8.una via ferrea tiene una pendiente de 8.7mm por metro¿que angulo forma con el horizonte?




9.la distancia entre dos puntos de un mapa es, conforme a la escala, 5km. si la recta que los une es un angulo de 9° con el horizonte,¿cual es al verdadera distancia que los separa?





10.desde la cima N de una roca de 40m de alto, se ve una boya anciada hacia el oeste, y el angulo de depresiones de 26°34´ ¿cual es le angulo de depresion xde otra boya B, situada al sur de la primera, si dista 23m de ella?



11.A,B y C son tres boyas. la boya B queda al norte de la A y C esta en la direccion norte-noroeste de la boya A ,hallese la distancia B a C sabiendo que de A a B hay 854m




12.un buque B esta navegando hacia el sur con una velocidad de 36km por hora, a las 12h un faro F se ve hacia el este y a las 12h 20m se le ve en la direccion norte-noroeste. hallar la distancia BF del buque al faro en el momento de la primera observacion



13.un observador halla que el angulo de elevacion de la cima de la torre, vista desde cierto punto A es de 28°;adelanta 30m hacia la torre,y entonces el angulo de elevacion D es de 47°¿cuantos metros le faltan para llegar al pie de la torre





14.desde la cima de una colina C,se ven dos mojoneras A y B, distantes de un kilometro, y los angulos de depresion son, respectivamente 8° y 16°¿que altura tiene la colina?(se suponen las mojoneras en un plano horizontal y en un mismo plano vertical con la cima)





15.una estatua DC esta colocada sbre una columna BD de 40m de alto . a una distancia AB de 25m de pie de la columna, la estatua se ve bajo un angulo de 5°¿cual es la altura de la estatua?



ANFONSSI FLORES MEYER, TRIGONOMETRIA RECTILINEA. SENO 48,49,50




calculese el cateto b sabiendo que:

1.a=26.45  B=37°20'



2.a=54.17  B=58°45'



3.a=32.27,  B=39°50´



4.a=52.56,   B=37°26´



5.a=125.34    B=49°37´



6.a=324.43,   B=17°30´



calculese la hipotenusa, sabiendo que:


7.b=42,   B=37°40´



8.b=56.48    B=75°20´




9.b=72.46,    B=35°40´




10.b=75,    B=35°43´




11.b=37.40      B=27°36´



12.b=125.54,   B=36°57´




calcular el angulo B, sabiendo que:


13.a=37.42   b=21.20



14.a=56.81    b=17.14



15.a=24.35      b=8.93



16.b=32.44      a=65.34



17.b=12.21    a=54.12



18.b=42,34    a=45.48




19.una escalera de 9m esta apoyada contra una pared.¿que altura alcanza si forma con el suelo,supuesto horizontal, un angulo de 72°?



20.se inscribe de un decagono regular en una circunferencia de 5cm de radio. calculese la longitud del lado de dicho poligono



21.¿cual es el radio de la circunferencia circunscrita a un heptagono regular de 2cm de lado?



22.se necesita conocer la distancia norte-sur de un terreno cercano. para eso traza las rectas ON y OS y se mide el angulo NOS, que resulta de 38°¿cual es la distancia si de N a O hay 300m y la recta NS es perpendicular a OS?



23.un obrero tiene una escalera de 12m¿que angulo debe hacerle formar con el suelo, si quiere alcanzar una altura de 9m?




24. la luz de un puente forma un angulo de 66°, correspondiente a una cuerda de 34m. calculese el radio de dicho arco



25.el angulo en la base de un triangulo isosceles es de 34°, y la altura mide 15m , calculese la longitud de cada uno de los lados iguales



26.supuesta la tierra esferica y el radio ecuatorial de 6378km , calcular la distancia BC del plano del tropico de cancer al plano del ecuador, sabiendo que los tropicos estan a 23°27' del ecuador



27.¿cuanto mide segun los datos del problema anterior, el radio DC de cada uno de los tropicos , y cual es la longitud de la circunferencia correspondiente?



28.¿cual es, en kilometros, la longitud de un arco comprendido entre dos puntos situado sobre el paralelo 48°50', si la diferencia de longitudes es de 15°?



29.¿cuantos kilometros hay que recorrer sobre el paralelo 40° para que el arco correspondiente sea de 10°?




ANFONSSI Y FLORES MEYER, TRIGONOMETRIA RECTILINEA. COSENO 51


CALCULESE EL CATETO c CON LOS DATOS SIGUIENTES:

1. a=36.42   B=38°


2.  a=75.47    B=49°35'


3. a=34.27     B=16°55'



4. a=126.45   B=78°44'



5. a=44.21   B=49°26'


6. a=134.80   B=77°26'



CALCULESE LA HIPOTENUSA, SABIENDO QUE:


7. c=25,   B=18°30´



8.c=37,  B=75°20'



9.   c=9.75   B=37°43'



10.  c=17.83,   B=76°35'



11. c=125,    B=64°28´



12.  c=21.79   B=35°45'


CALCULESE EL ANGULO B EN LOS TRIANGULOS RECTANGULOS EN QUE:

13. a=37,  c=18.23


14.  a=45.32,  c=30.25


15.  a=.27     c=.12


16.  a=135  c=57



17. El pie de una escalera de 10m  , apoyada contra una pared , queda a 3m de esta ¿que angulo forma la escalera con el suelo ?



18. una cuerda subtiende un arco de 48°¿cual es la longitud de su flecha  si es el radio es de 5cm?



19.¿cual es la longitud de la apotema y el area de un eneagono regular inscrito en una circunferencia de 24cm de radio?


20. la base de un triangulo isosceles mide 4cm, y cada uno de los lados iguales es de 5cm. calcular cada uno de los angulos de la base



21. para obtener la longitud de la huerta representada , se a medido el angulo CAB, que es de 33°, y la distancia AC=276m ¿ que longitud tiene la huerta?



22.Un barco, navegando desde P hacia el noroeste, a llegado al punto A, distante a 25km de I .supuesta plana la superficie de las aguas, ¿ a que distancia AB se halla de la direccion norte-sur del punto de partida?



ANFONSSI Y FLORES MEYER, TRIGONOMETRIA RECTILINEA . TANGENTE  52,53

CALCULESE EL CATETO B CON LOS DATOS SIGUIENTES:

1. c=14.24   B=36°30´


2. c=17.84   B=74°50´


3. c=27.73  B=30°40'


4.  c=19.69   B=80°10´


5. c=18.40  B=25°37´


6.  c=42.51   B=48°53'


7.  c=132.4   B=75°37'


8. c=140.8   B=19°48'


calcular el angulo b, sabiendo que:

9.  b=16.21    c=14.23


10. b=89.40  c=15.31


11.  b=132.4   c=23.48


12.  b=144.5  c=89.20


13.  b=17.48   c=19.85


14. b=19.50   c=37.56


15. b=56.37   c=136.25


16,  b=75.80   c=276.2


17.calcular el angulo en la base de un triangulo isosceles, sabiendo que dicha base mide 36m y la altura es de 14.28m


18. calcular el lado de un dodecagono regular cinscuncrito a una circunferencia de 3cm de radio.



19.calcular el radio de la circunferencia circunscrita a un punto decagono regular  de 4cm de lado


20. un arbol de 17m de altura , proyecta una sombra de 25m. ¿ a que altura se halla el sol sobre el horizonte del lugar?


21. ¿bajo que angulo se ve un arbol de 12m de alto a 43m de distancia?


22.¿que angulo forma la visual del sol sobre el horizonte de un lugar en el momento en que la longitud de la sombra proyectada por un edificio es doble de su altura?



CALCULESE EL CATETO C CON LS SIGUIENTES DATOS:

1.  b=24.32   B=25°40'


2. b=34.25   B=48°50'


3.  b=75.36   B=74°20'


4.  b=42.57   B=40°50'



ANFONSSI Y FLORES MEYER, IDENTIDADES Y ECUACIONES 127,131


FUENLABRADA , SAMUEL GEOMETRIA Y TRIGONOMETRIA ED.MCGRAW HILL IDENTIDADES 119,12O

FUENLABRADA, SAMUEL GEOMETRIA Y TRIGONOMETRIA. ED. MCGRAW HILL ECUACIONES 135,136


ANFONSSI Y FLORES MEYER LEY DE SENOS Y COSENOS . PAGS 161,162


GUIA DE MATEMATICAS 2. COBAO. PAGS. 134,136, 147 RT

GUIA DE MATEMATICAS 2. COBAO. PAGS. 148,149 RT

GUIA DE MATEMATICAS 2.COBAO. PAGS.155 RT


GUIA DE MATEMATICAS 2. COBAO.PAG.187 IDE

GUIA DE MATEMATICAS 2.COBAO.PAGS.191,192 IDE

GUIA DE MATEMATICAS 2. COBAO. PAGS. 211,212TO